一道老题

　　学弟问我的一个题目，去年本来做过，但是做的稀里糊涂，今天拿出来重新推导了一遍，特记录于此。
　　题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2971
　　先假设a2 = t, 题目给定了递推关系：An = 2 * t * An-1 - An-2 (n > 2)，初值A1 = 1, A2 = t；题目要求Sn = An ^ 2 + An-1 ^ 2 + ... + A1 ^ 2。
　　反复应用递推关系得到：
　　
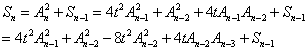
　　然后Sn-1利用相同的方式展开，把4tAn-2An-3约去，得到：
　　
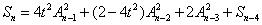
　　这样就比较容易得出Sn的通项：
　　

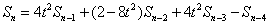
　　当初这个题目之所以没想到这种方法，就是因为一看到递推关系，就想着用一般解方程的方法去求解通项，思维被局限了，其实用简单的方式就可以推出来的。以后对于一个问题，应该从多个方面去想，不能想当然啊。想起最近看到的一段话，以此自勉：
　　正则表达式非常强大，但是它并不能为每一个问题提供正确的解决方案。你应该学习足够多的知识，以辨别什么时候它们是合适的，什么时候它们会解决你的问题，什么时候它们产生的问题比要解决的问题还要多。
　　一些人，遇到一个问题时就想：“我知道，我将使用正则表达式。”现在他有两个问题了。——Jamie Zawinski